Math behind Back-Propagation

Today let’s demystify the secret behind back-propagation. In this post, I will try to include all Math involved in back-propagation. Familiarity with basic calculus would be great. Otherwise, I don’t recommend continuing this article.

Let’s start with what is back-propagation? In simple terms, it computes the derivatives of the loss function with respect to weight and biases in a neural network. Algorithms such as gradient descent or stochastic gradient descent use gradient computed through back-propagation for optimization. That’s it for the intro, let’s dive into the Math.

Let‘s find the derivative of the softmax, this is something that we need later. We can apply Quotient rule to find derivative, since it is in the form g(x)/h(x).



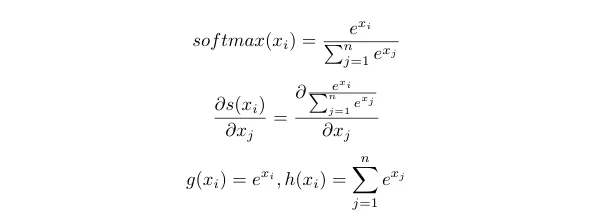
There will be two cases, i equal to j and not equal to j.



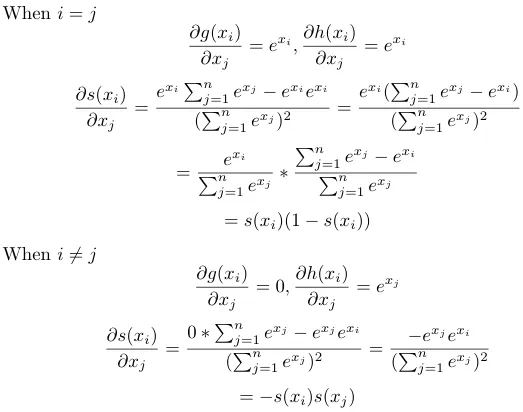
Till now we haven’t computed any gradient w.r.t loss, we are building to it step by step.

Let’s consider the neural network shown blow.

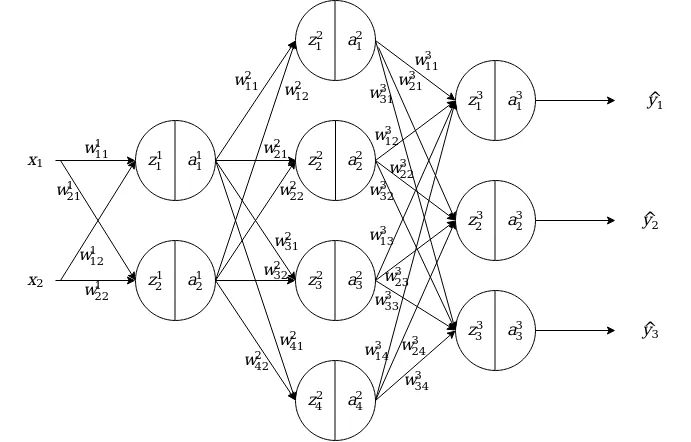
z is the weighted sum of activation of the previous layer and corresponding weights and a is the activation of the neuron which is obtained by applying activation function to z. Now let’s look, how activation of a specific neuron is represented.



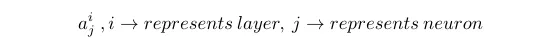
The above example represents the activation of 2nd neuron in 3 layer.

It is time to get into the meat and flesh.

Let’s find the derivative of loss w.r.t z in the output layer(l th layer). As I already mentioned, cross-entropy will be our loss.



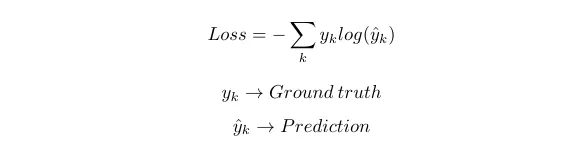
k is the number of predictions, it will be equal to the number of neurons in the output layer.

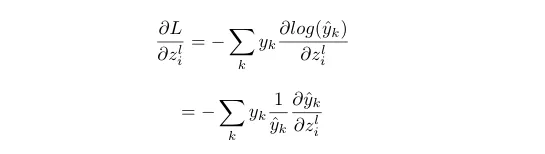
We can use the derivative of softmax that we derived earlier. One thing to remember, we need to compute the derivative of softmax k times in which k-1 times i is not equal to k.

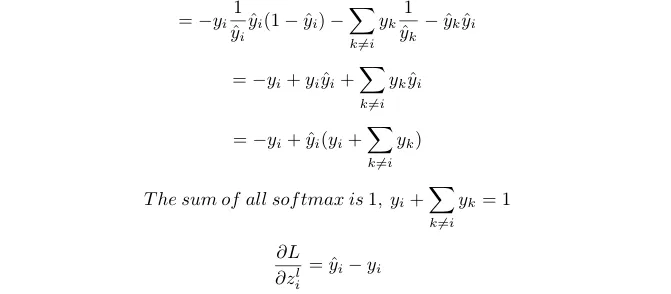
Let’s continue our derivation considering the above network.

Now let’s find the derivative of weights with respect to loss, we will be using chain rule here.

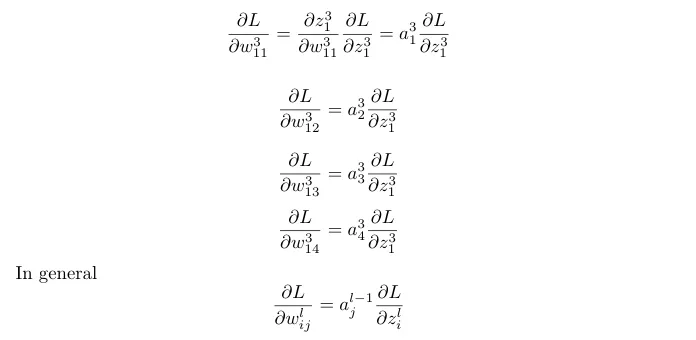
Bias units are not shown in the network, but they are present in the network.



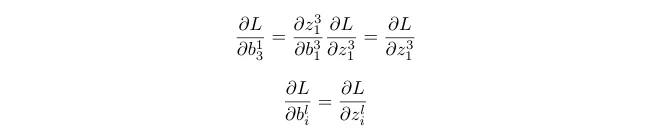
Derivative of activation in the previous layer are as follows.

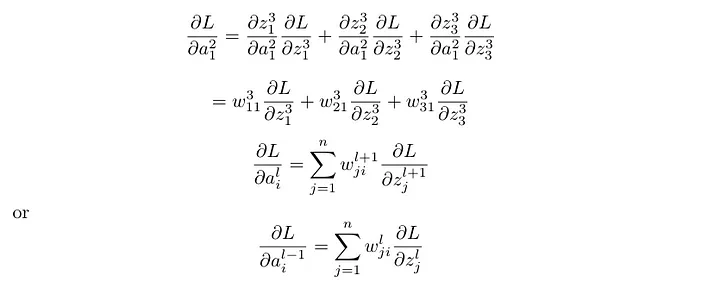
Here n is number of neurons in the current layer.

Let’s look at the derivatives of z in the hidden layer w.r.t loss.



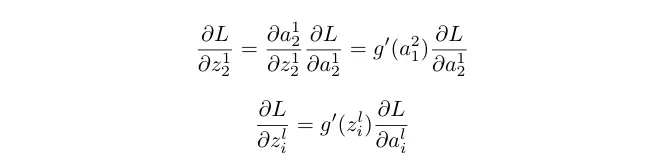
Here g’(z) is the derivative of the activation function used in the corresponding layer.

We have formed general equations to find the derivative of weights, bias and activation w.r.t loss.

The process of finding derivatives is as follows. We will first find the derivative of the last layer w.r.t loss then will use these derivative to find derivative of the second last layer, this process will continue until the input layer. This how back-propagation computes derivatives. Here the flow is from last to the first layer, which directly opposite to forward propagation.

Hope you enjoyed it. If you’ve made it this far and found any errors in any of the above or can think of any ways to make it clearer for future readers, don’t hesitate to drop a comment. Thanks!